Tag: South

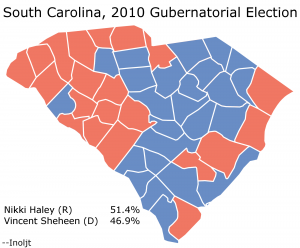
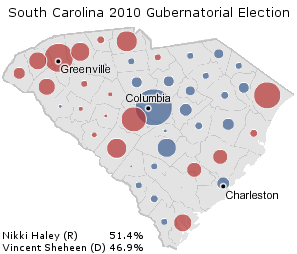
This is part of three posts analyzing the 2010 South Carolina  gubernatorial election, in which Republican Nikki Haley won a  closer-than-expected victory over Democrat Vincent Sheheen. The main  focus of these posts will be to explore whether a racial effect  accounted for Ms. Haley’s unexpected poor performance.

(Note: This is also part of a series of posts analyzing the 2010 midterm elections.)

More below.

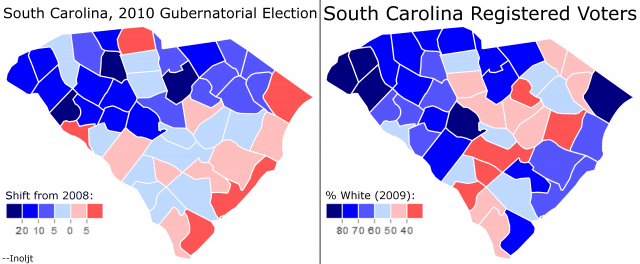
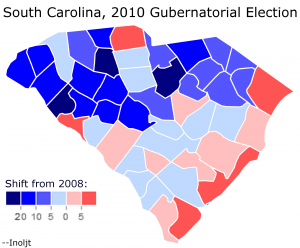
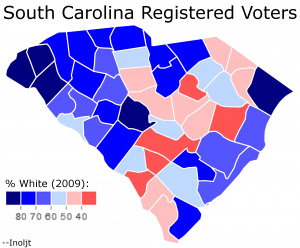
The previous post mapped out the relationship between Democratic shifts in 2010 and white registration numbers. Here is the relevant map reposted:

The post ended by noting that “So far this analysis has been relatively light on the statistical side of things.” It included a number of maps, but did not use any raw numbers.

This post aims to draw conclusions based on those numbers.

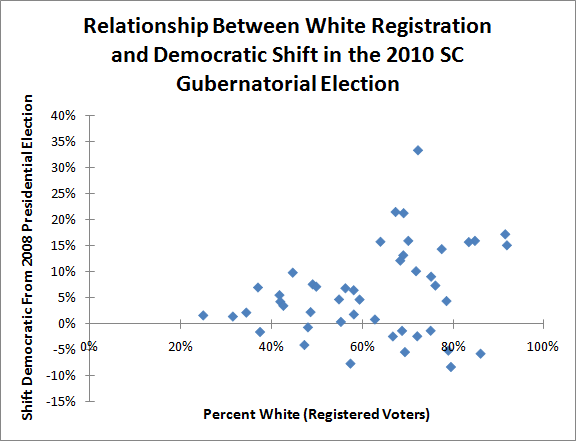
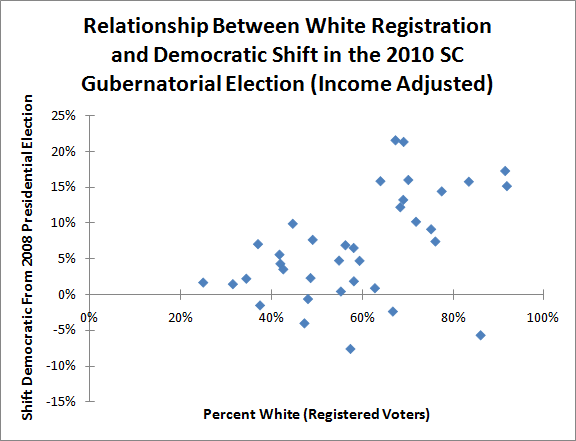
Let’s begin by translating the picture above into a graph:

This graph maps the relationship between how white a county in South Carolina is, and how much it shifted against non-white Republican candidate Nikki Haley in 2010.

If normally-Republican whites moved against Ms. Haley due to her race, one would expect the dots to be graphed in a roughly 45-degree diagonal line; the whiter a county, the more Democratic it would shift in 2010.

Clearly this is not the case in the graph above. There are a lot of very white counties that shifted strongly against Ms. Haley – but there are also a lot of very white counties that supported her more than they did Senator John McCain.

Indeed, the whitest counties seem to spread out into two groups; one group moves strongly against Ms. Haley, another actually shifts for her. One might speculate that the former group is composed of lower-income, rural whites and the latter is composed of higher-income, metropolitan whites.

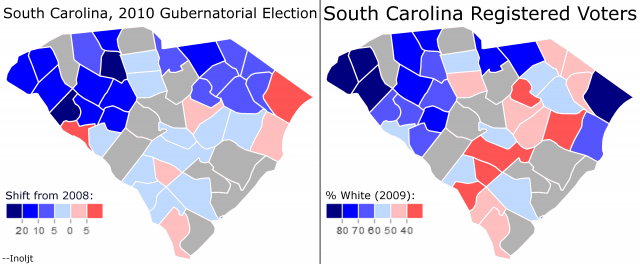
To test this theory, the previous post adjusted for income by eliminating all the counties with a median household income greater than the state median (i.e. it got rid of the rich whites). Here is what the result looked like:

There seems to be a correlation here, as the previous post noted.

Here is how the relationship looks on a graph:

The group of white counties which shifted towards Ms. Haley has disappeared. Instead, one sees a much stronger trend: the whiter the county, the more strongly it moved against non-white Republican Governor Nikki Haley.

This only happens once high-income white counties are tossed out of the analysis. High-income Republican whites were very comfortable voting for non-white Republicans; low income Republican whites were less willing.

Interestingly, this pattern is not unique to South Carolina. In Louisiana, Republican Governor Bobby Jindal – a non-white individual of Indian descent – did extremely poorly amongst rural, low-income (Republican) whites while winning landslide support amongst high-income, suburban (Republican) whites. This caused Mr. Jindal to lose in his first attempt to run for governor.

Finally, one can test whether the effect above is statistically significant, or just the result of randomness.

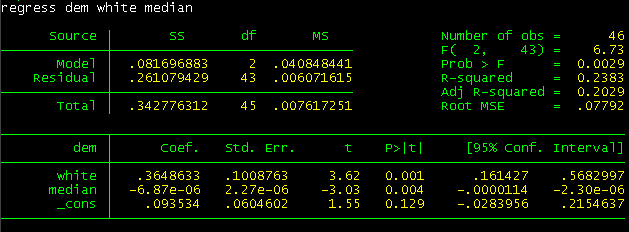
Here is a regression analysis run on the 2010 South Carolina gubernatorial race:

Regression analysis is something I am still not fully comfortable with, so bear this in mind as the analysis continues.

The regression attempted to use two variables – race and income – to predict whether voters would vote more Democratic in 2010. Specifically, it used the percent of white registered voters in a county and said county’s median household income.

The model states that every 10% increase in white registered voters results in a 3.65% greater Democratic shift against Ms. Haley (this is the Coefficient column at the bottom left).

More importantly, whiteness and income were statistically significant when placed together; there was a 0.1% chance that the effect of whiteness was random, and a 0.4% chance that the effect of income was random (this is the P>|t| column at the bottom center).

So the evidence is fairly strong that racially-based voting by low-income whites hurt non-white Republican Ms. Haley in 2010.

There is, however, a caveat. The above regression only explains 20% of the variance between the different degrees of Democratic shifts between different counties (this is the Adj R-Squared line at the top right). This means that 80% of the variance is not explained by race and income.

Racism probably hurt Ms. Haley in 2010, but it was far from the only factor.

–Inoljt

.

.

.

P.S. Here is the relevant data used to built this analysis:

County	% Change   Democratic	% White   Registered	Median   Household Income
Abbeville	21.31%	69.08%	33,995
Aiken	-1.30%	75.02%	43,845
Allendale	1.65%	25.09%	23,942
Anderson	15.75%	83.40%	41,399
Bamberg	-1.54%	37.56%	28,266
Barnwell	0.40%	55.31%	30,549
Beaufort	-8.27%	79.47%	54,085
Berkeley	-1.32%	68.74%	49,609
Calhoun	4.72%	54.90%	39,537
Charleston	-5.41%	69.36%	46,145
Cherokee	14.40%	77.45%	35,807
Chester	4.69%	59.40%	33,640
Chesterfield	15.82%	64.00%	32,267
Clarendon	2.28%	48.66%	29,840
Colleton	1.83%	58.16%	35,935
Darlington	6.87%	56.31%	34,577
Dillon	7.62%	49.11%	28,653
Dorchester	-2.37%	72.07%	52,443
Edgefield	0.86%	62.79%	38,885
Fairfield	4.28%	42.02%	32,694
Florence	6.49%	58.12%	39,919
Georgetown	-2.40%	66.73%	40,573
Greenville	4.41%	78.49%	45,917
Greenwood	12.18%	68.35%	39,586
Hampton	3.50%	42.67%	32,253
Horry	-5.72%	85.98%	41,163
Jasper	-4.05%	47.30%	35,163
Kershaw	33.41%	72.24%	45,268
Lancaster	9.10%	75.12%	40,286
Laurens	10.15%	71.81%	36,910
Lee	7.02%	37.11%	28,041
Lexington	15.99%	84.74%	52,062
Marion	5.55%	41.82%	28,437
Marlboro	9.87%	44.75%	26,799
McCormick	-7.63%	57.41%	35,557
Newberry	13.21%	69.01%	37,263
Oconee	17.25%	91.39%	39,840
Orangeburg	2.19%	34.54%	33,567
Pickens	15.13%	91.76%	40,357
Richland	7.18%	49.90%	45,643
Saluda	15.99%	70.11%	40,819
Spartanburg	7.39%	76.07%	40,278
Sumter	-0.65%	48.08%	37,113
Union	21.54%	67.31%	32,361
Williamsburg	1.43%	31.59%	26,639
York	-5.13%	78.89%	50,644
Total	4.52%	69.66%	42,580

This is the second part of three posts analyzing the 2010 South Carolina  gubernatorial election, in which Republican Nikki Haley won a  closer-than-expected victory over Democrat Vincent Sheheen. The main focus of these posts will be to explore whether a racial effect  accounted for Ms. Haley’s unexpected poor performance.

The previous post can be found here, and the next post can be found here.

(Note: This is also part of a series of posts analyzing the 2010 midterm elections.)

More below.

How to Find a Racial Effect

The purpose of this series of posts is to determine whether or not Ms. Haley’s relatively weak performance was due to a racial effect.

In order to due this, it’s necessary to define what to look for. In this case, it would be normally Republican voters abandoning Ms. Haley due to her race.

Now, South Carolina is a state in which less than 5% of the population is neither white nor black; minorities other than blacks play a negligible role in the state’s politics. It is also a very racially polarized state, like most places in the  Deep South. Blacks vote Democratic; whites vote Republican.

There is one final factor to take into account. When Republican Bobby Jindal ran for governor in 2003 and faced racially-based opposition by (white) Republicans, such opposition was not evenly distributed. The Republicans who abandoned Mr. Jindal tended to be predominantly from rural, relatively lower income areas. This is something that is not especially surprising, although it conforms to some unfortunate stereotypes.

For these reasons, an examination of Republicans who abandoned  Ms. Haley for racial reasons would look specifically at areas with lower-income whites. These areas would be expected to shift more Democratic than the norm.

Democratic Shifts

To begin this post, let’s examine the places where Republicans improved upon their 2008 performance, and the places where Democrats improved upon 2008.

Naturally, given that Ms. Haley did worse than Mr. Sheheen, one would expect Democrats to have relatively more improvement.

This turns out to be the case:

Here one sees a very interesting regional pattern, a pattern that I did not expect when making this map.

The northern parts of South Carolina moved strongly Democratic in 2010. The sole exception is York County, which for whatever reason shifted Republican (there is, strangely enough, very little that differentiates this county with others in the region; nor did either Ms. Haley or Mr. Sheheen represent the county as politicians before 2010).

On the other hand, the coastal regions actually supported Ms. Haley more than they did Senator John McCain.

This is a very interesting regional divide; it is something that is entirely hidden by normal partisan patterns.

Whites

Now, let’s take a look at white registration figures:

This map shows what percent of South Carolina’s registered voters are white. The information is mandated by the Voting Rights Act, given South Carolina’s history of preventing minorities from voting, and can be found at this website. It is also quite useful for the purposes of this analysis. (For fun: compare this map to President Barack Obama’s performance).

In order to make comparisons easier, the same color scale was used in this map as in the previous map. The whiter a county’s voter population, the bluer the county on the map.

If white Republican voters rejected Ms. Haley due to her race, then the whitest counties here would also have the strongest Democratic shift (i.e. the colors in each map would roughly match).

Let’s compare the maps:

There is a bit of a match, but not much. A lot of very white counties shift strongly against Ms. Haley, but a lot of them also shift strongly for her (especially along the coast).

One can reasonably conclude that a lot of white voters – i.e. Republicans – remained loyal to Ms. Haley despite her Indian heritage.

This is not entirely unexpected. Mr. Jindal also retained a large amount of white support, mainly amongst suburban and wealthy whites.

Adjusting For Income

Where Mr. Jindal did especially poorly – and why he lost the 2003 gubernatorial election – was amongst rural, lower income whites in Louisiana.

Let’s therefore shift this analysis by adjusting for income; in other words, by focusing upon lower-income counties in South Carolina.

South Carolina’s median household income was $42,580 as of 2009, according to Census Data (which can be accessed here).

One can therefore adjust for income by restricting the analysis only to those counties in which median household income was below the state median.

This is what happens:

This looks like a far stronger relationship. In the poorer parts of South Carolina, it appears that the whiter the county, the more against Ms. Haley it shifted.

It seems that we have found something here.

So far this analysis has been relatively light on the statistical side of things; it kind of looks like there is a pattern in the map above, but perhaps there isn’t one. How likely is it that this could have occurred by chance?

The next post will answer this question.

–Inoljt

This is the first part of three posts analyzing the 2010 South Carolina gubernatorial election, in which Republican Nikki Haley won a closer-than-expected victory over Democrat Vincent Sheheen. The main focus of these posts will be to explore whether a racial effect accounted for Ms. Haley’s unexpected poor performance.

The next post can be found here.

(Note: This is also part of a series of posts analyzing the 2010 midterm elections.)

More below.

It was the October, 2010 in South Carolina. Nikki Haley, Republican candidate for South Carolina governor, was cruising. She was a conservative candidate – endorsed by none other than Sarah Palin herself – running in a conservative state, in the best Republican year in a generation.

Opinion polls showed the Republican politician leading by double-digits. Even the most pessimistic gave Ms. Haley a high single digit lead.

On election day, however, Ms. Haley won by only 4.5%:

(Note: Edited NYT Image)

What could have accounted for Ms. Haley’s poor performance?

Several factors come to mind. Ms. Haley was not an uncontroversial candidate; her positions were conservative even for South Carolina. The Democratic candidate, Vincent Sheheen, might have been an unnaturally talented campaigner. And there is always the factor of randomness to take into account. There were hundreds of races in November; the polls would inevitably be inaccurate on one or two, and this race just happened to be one of them.

Or perhaps there is another explanation – a particularly ugly one, but one that lurks at the back of everybody’s head. Ms. Haley was an woman of Indian heritage running to govern South Carolina, a state with not exactly the most innocent racial history. Throughout the campaign, Ms. Haley was subject to attacks that implicitly played up the racial angle: she had had affairs with white men (unfortunately for the accusers, this attack doesn’t work as well against women), she wasn’t Christian or was only pretending to be one, and so on.

It is not unimaginable that a sort of Bradley effect took place in South Carolina, that a number of normally steadfast Republicans balked at voting for the first non-white and female governor in history.

This is a serious accusation, and therefore needs serious evidence. The next post will therefore begin an extensive examination of whether Ms. Haley’s race undermined her performance.

–Inoljt

Drawing from a rather long comment I had on a previous diary, I’ve decided to expand my one part diary on redistricting in the Bayou State to two.

The first part will run through recent developments in state politics and who controls the redistricting process, while the second will include my proposed map for Louisiana’s 6 congressional districts.

In my honest opinion, Louisiana is the state least alike the other 47 states that make up the continental United States.

Administrative subdivisions are called parishes, not counties. It is a civil law state, as opposed to the other 49 common law states.

Politics in the state are no different.

Party labels are very fluid. In state government, there are conservative Democrats – although less so now – and some fairly moderate Republicans, especially for standards of the Deep South.

In the past few months, Democrats have taken a hit, and in Louisiana, it has been no different.

For the first time since Reconstruction, Republicans control the state house. There is a Republican governor, and after Attorney General Buddy Caldwell’s party switch last week, the only statewide elected Democrat is Sen. Mary Landrieu.

That leaves the state senate, which currently is split right down the middle, 19 Democrats and 19 Republicans.

This gridlock is a result of party switchers, notably state Sen. John Alario, and a single vacancy.

Redistricting in the state is done by the legislature and the governor and it seems the last chance for Democrats to be at the table, outside the Holder DOJ, is the state senate.

Let’s look at that vacancy.

The 26th district is vacant after Sen. Nick Gautreaux resigned to become Bobby Jindal’s commissioner of the Office of Motor Vehicles.

(Just an aside, this appointment and that of a former independent state senator as the Commissioner of the Office of Alcohol and Tobacco Control was smart politically by the governor and is VERY reminiscent of President Obama’s appointments of Jon Huntsman and John Mchugh)

The 26th district includes all of Vermillion parish and parts of Acadia, Lafayette and St. Landry parishes.

The district takes in areas of Cajun country west of Lafayette and stretches down south to include Vermillion parish, ending at the Gulf. To better understand the region, the 2000 census reported about a quarter of people in Vermillion speak French or Cajun French at home.

This area is historically Democratic. In the jungle primary in the 2003 gubernatorial election, 3 of the 4 parishes in district 26 were won by Kathleen Babineaux Blanco, who would win only 7 parishes and grab only 18% of the vote but squeak into the general election against Bobby Jindal.

This small chunk of Acadiana will decide which party will control the state senate.

After Gautreaux’s announcement that he would resign, Republican state Rep. Jonathan Perry, who represents much of the sparsely populated coastal parts of Vermillion and Cameron parishes, entered the race.

Soon thereafter, Democrat Nathan Granger, a member of the Vermillion Parish Police Jury and owner of an oilfield services company, entered the race.

At this stage in the race, both camps have released dueling internals showing each with about a 10 point lead.

Anecdotally, I have heard from a friend from Crowley that the area is swamped with advertisements from Granger and after reviewing campaign finance reports, it appears that is the case.

As of Jan. 31, campaign finance reports show Granger raised about 280k, of which 220k was self-funded, with 100k COH.

Perry has raised 90k and has 30k COH.

Take all this with a grain of salt, but it appears that this Blue Dog might just dispatch a Tea Partier in a very important race for Louisiana politics.

In part 2, the map I unveil will show why Democrats need to have a seat at the redistricting table as I attempt to create a VRA district based in New Orleans that DOES NOT stretch all the way to Baton Rouge.

For purpose of this discussion, I’ve included the following states as “Southern”.  They are TX, LA, MS, AL, FL, GA, SC, NC, VA, TN, KY, and AR.  I left out some states such as MO,WV, and OK, where some would include as part of the South.  I think they are better suited elsewhere.

After the 1970 House elections, the Democrats had a whopping advantage of 84-29.  Here are the numbers for the following elections:

1972 Dems 79-36 edge

1974 Dems 86-29 edge

1976 Dems 86-29 edge

1978 Dems 81-34 edge

1980 Dems 73-42 edge

1982 Dems 86-37 edge

1984 Dems 77-46 edge

1986 Dems 81-42 edge

1988 Dems 81-42 edge

1990 Dems 81-42 edge

1992 Dems 81-50 edge

1994  GOP 68-63 edge

1996  GOP 76-55 edge

1998  GOP 76-55 edge

2000  GOP 77-54 edge

2002  GOP 81-56 edge

2004  GOP 87-50 edge

2006  GOP 81-56 edge

2008  GOP 76-61 edge

As a note, it’s interesting that under Jimmy Carter’s presidency, we lost (net) 13 seats and under Clinton we lost (net)27 seats.

Back in the 1970’s and 1980’s, it was quite acceptable for a Southerner to vote for a Democrat.  Some of it has to do with the old Yellow Dog mentality (or better yet, because of some silly argument that Lincoln ruined the South).  Anyway, when the Dems had a large advantage in the South, there were very few who would be called a true progressive, albeit a liberal.  Yet, they did provide some assistance in some progressive economic issues.  Around 1992, many Southerners truly demonized Bill Clinton, saying that his morals and his big-government friends were going to ruin the US.  The moral majority joined the fray by stressing cultural issues that were imortant to many Southerners.  It’s somewhat ironic that it was under a Southern President’s watch that the GOP gained a stronghold of the South.

There have been plenty of party switching during the last 38 years, with many conservative Dems leaving the party and joining the GOP ranks.  The last time we had a US rep from the South leave the party was in 2004, when Rodney Alexander of LA and Ralph Hall of TX left the party.  I’m hoping the exodus from our party is over.

Currently, we have 21 Blue Dogs that reside in the South:  4 in GA (Barrow, Scott, Bishop, Marshall), 2 in AR (Berry, Ross), 1 in FL (Boyd), 2 in AL (Bright, Griffith), 1 in KY (Chandler), 2 in MS (Childers, Taylor), 4 in TN (Cooper, Davis, Gordon, Tanner), 1 in TX (Cuellar), 2 in NC (McIntyre, Shuler), 1 in LA (Melancon), and 1 in VA (Nye).

Most of these Reps are culturally conservative, but some are willing to help the Democratic party on economic issues.  Even a few (ex. Shuler) will vote for some pro-environment legislation.  Yet, many of us on SSP have mixed feelings about the Blue Dogs.  We like them for being in our ranks and occassionally supporting some progressive legislation, but then we get quite mad on other issues (cultural issues, healthcare, etc.).  So what should we do with the Blue Dogs?

First, if the current Blue Dogs in the South bolted our party, the GOP would have a huge advantage (97-40).  That, my friends, is shocking, since prior to the civil rights act of 1964, there were only a handful of Republicans in the South.  

Anyway, I wanted to open this up to discussion, because the South could end up losing several Democratic Rep seats in 2010.  My questions are:

1.  Are we willing to support Blue Dogs in the South when very vew are willing to support us on key issues (i.e. healthcare)?

2.  Is there a way to triangulate our ideas with the Blue Dogs whereby we can get some meaningful legislation passed without having to “water down” the importance of the legislation?

Looking at the county returns from the 2008 Presidential election, Obama made impressive gains almost across the board.  The one exception to the trend, as we’re all aware of around here, is in the Yellow Dog Democrat counties of the southern Midwest, Deep South, and Appalachia.  While these counties have been trending against the Democrats for decades, and particularly since the Clinton years, the Yellow Dog realignment into the waiting hands of Republicans was almost 100% completed in the 2008 election.  The question is….can we ever get them back in national elections?

Not everyone’s definition of Yellow Dog Democrats is the same, but I usually classify them as the conservative Democrats of the three aforementioned regions (Appalachia, southern Midwest, Deep South) in majority-white jurisdictions.  On the surface, Obama’s 29 county victories in Mississippi suggest a continued presence of Yellow Dog-ism, but nearly all of those 29 counties are majority-black.  One of the last-standing Mississippi counties that could be generously classified as a Yellow Dog County is Benton County in the north-central part of the state, and that was the only 2004 Kerry county in the state to swing to Bush this year.

As a rule, the smaller the minority population in a given county, the more likely they were to see a seismic movement towards McCain this year compared to past Presidential elections.  The Mondale-McCain counties chart on this website outlined this realignment quite effectively, but the role race played in harming Democratic chances in many of these counties is likely quite substantial.  Had Hillary Clinton been the nominee, it’s probably a safe bet that the Mondale-McCain county list would have fewer entries, particularly in states like Kentucky and Tennessee.

Kerry took a substantial hit in the Yellow Dog Democrat counties four years ago as well, but I’m struck how many of the now seemingly long-gone Yellow Dog counties were still onboard for Al Gore, even outside of Gore’s home state of Tennessee.  There were two counties in southern Illinois (Franklin and Perry) where Gore was victorious but favorite son Barack Obama couldn’t even pull out a win.  The same is true in a handful of counties in western Kentucky and northern Alabama.  It’s hard to imagine that any high-profile national Democratic figure could emerge victorious in 2008 in Gore counties like Ballard County, Kentucky; Jackson County, Alabama; and Hughes County, Oklahoma.

It strikes me that the significance of so many of these counties holding on through the 2000 Gore v. Bush election can be at least somewhat connected to that election being more senior-centric than any campaign in recent memory (“putting Social Security in an ironclad lock box”).  It can be safely assumed that it was the oldsters in these mostly rural Yellow Dog counties who were most likely to stick with Gore in 2000 and who have dying off in years since.  Those still alive are statistically the demographic most likely to be repelled by the prospect of an African-American for President.  But in some cases, the shift away from Obama was so dramatic this year that it leaves me wondering if the Democratic proclivity in the Yellow Dog counties has been completely abandoned by younger generations of residents.  Are the allegedly more tolerant 20-somethings of Letcher County, Kentucky, just as likely to forfeit their Democratic heritage as their grandfathers over race?  Or has the Democratic heritage been diluted over the generations to the point that the 20-somethings have no emotional or familial ties to the Democratic Party.

Interestingly, at the time I thought Gore’s 2000 showing represented the Democratic trough as it pertained to the Yellow Dog regions, at least in northern Appalachain Clinton strongholds like eastern Ohio, western Pennsylvania, and West Virginia.  Certainly, I thought, the squishy Gore margins in this region merely represented a one-time flirtation with a “compassionate conservative” that was produced by Clinton exhaustion.  I felt the same about the Upper Midwest after Gore’s soft showing in that region, and went into 2004 expecting Kerry to vastly overperform Gore everywhere from Aberdeen, South Dakota, to Decatur, Illinois, to Steubenville, Ohio.  I ended up being stunned to see many of these areas actually got redder in 2004.  And then of course in 2008, the trajectory of the two pro-Bush regions split.  Obama saw considerable gains in the Upper Midwest and Corn Belt while the Yellow Dog strongholds continued their drift towards Republicans.

With that in mind, looking forward to 2012, the question begs itself….can these people be won over?  If Obama gets as high of marks for governing in the next four years as he has for organizing his campaign and transition team in the last two, will the voters of Hope, Arkansas, be less afraid than they are now of “blacks taking over the levers of power in the country” after attaining the White House?  If the insane fears of Obama’s “Muslim background” are proven fruitless in the next four years, will Al Gore’s former neighbors in Carthage, Tennessee, resume their long-standing tradition of instinctively voting Democratic in future election cycles?  If serious efforts are undertaken (and ideally delivered) to reverse the decline of the lower-middle class, will the voters of Weirton, West Virginia, reconnect with the Democratic Party they were so solidly aligned with in the past century?  Or is the drift towards Republicanism in these areas irreversible for the foreseeable future now matter how well Obama performs in office?

I split the country into six regions for political analysis purposes.  Three of the regions trend Democratic (Northeast, Pacific, Great Lakes) while three favor the GOP (Plains, Mountains, South).  For purposes of this discusssion, I track House seats (number D, number R, % D), Senate seats (number D, number R, % D), Governorships, and Presidential voting in 2004 as well as the number of Bush Dogs (per the list on Open Left) and the percentage of the region’s House Democrats who are Bush Dogs.

Not surprisingly, the more solidly Democratic a region is, the less likely it is to elect a Bush Dog Democrat.  Only two of the Northeast’s 68 House Democrats are Bush Dogs (2.9%) while 19 of 58 Southern Democrats are Bush Dogs (32.7%).

The Northeast is the most solidly Democratic region in the country and seems to be swinging even more blue.  The region has the most House Democrats (68), the greatest number of Democratic pickups in 2006 (12 House seats/ 11 GOP House seats lost), and every one of the 11 states plus the District of Columbia went for Kerry in 2004.  It even claims the greatest number of governorships (9) and the highest percentage of Democratic governors (81.8%).

Surprisingly, the Northeast still offers Democrats a lot of opportunities in 2008. The region ‘s 24 House Republicans continue to scatter.  Five have announced they will not run for re-election and a sixth, Wayne Gilchrest, has been defeated in a primary by a right wing Club For Growth candidate in Maryland.  

One can make a case against Vito Fossella (NY-13) who faces a voter registration deficit and has less cash than a possible general election opponent.  Scott Garrett (NJ-5) is an extremist who has been slowly sinking since first elected. Jim Gerlach not only comes from a tough district but from one of only five GOP-held districts in which George W. Bush got a lower percentage of the vote against John Kerry than against Al Gore.

Democrat Eric Massa has more money than Randy Kuhl in NY-29 and gave Kuhl a tight race as a virtual unknown in 2006.  Jim Himes has also outraised  Chris Shays who is looking at his third nail biter in a row with a lot less national bucks to go around.  Frank LoBiondo’s Jersey district (NJ-2) has a Democratic lean and several promising local candidates are available and might be enticed into the race.  Sam Bennet in PA-15 has a similarly friendly district and a relatively weak opponent.  Peter King is also defending a tough district as the last Republican from Long Island.  He, too, has no opponent as of yet but the rumors are less encouraging for local Democrats.

Add it all up, and the Republicans are looking at perhaps ten safe seats in this election in an 11 state region.  And any Democrat elected is likely to be a moderate to full out progressive.  The only two Bush Dog Democratys from the region represent rural districts tin Pennsylvania that are not culturally part of the region.

The Pacific states are almost as friendly on the Presidential level as the northeast with only Alaska’s three electoral votes going for George W. Bush.  That disguises a deep divide between the Democratic coastal regions and the Republican interiors. The region has the second highest percentage of Democratic House members (46 D, 24R, 65.7%) and the second lowest percentage of Bush Dog Democrats (2 of 46, 4.3%).

The contrast between the Northeast in 2006 and the Pacific was startling.  Democrats in the region had high hopes but managed to pick up just one seat (Jerry McNerney defeated Richard Pombo).  Democrats came close but came away empty in WA-8, CA-50, and CA-4.  This cycle’s top targets include WA-8, CA-4, and AK-At Large. Two of the region’s three Republican Senators, Oregon’s Gordon Smith and Alaska’s aging and heavily investigated Ted Stevens are also being challenged this go around.

Three or four California House seats ooze corruption and should have at least the potential to be competitive but, as of this time, I am not too optimistic about seats like CA-50 (Bilbray), CA-26 (Dreier), CA-46 (Rohrabacher), CA-45 (Mary Bono Mack), or CA-49 (Issa).

The Great Lakes is the least Democratic Democratic region.  In fact, heavy gerrymanders by the GOP in Ohio and Michigan gave the GOP the slight edge in the region’s House selegations until Bill Foster’s election to Denny Hastert’s old seat in the special election.

One of the really encouraging things in this region is that a great number of GOP seats stayed on the table after 2006.  Republicans may have held on but they retired in droves leaving huge openings in Illinois and Ohio.  Hastert’s seat has already flipped and the 38-38 Democratic edge will likely expand.  Democrats have a great shot in OH-15 and certainly a good chance in OH-1, OH-2 and OH-16.  At least two GOP Michigan seats (MI-7, MI-9) are being vigorously contested this cycle and seats like IL-18, IL-11, and IL-6 are up for grabs. Jim Ramstad’s old seat in Minnesota is possible and some people seem to think that Michelle Bachman’s seat (MN-6, I think) is also in play.

Last cycle, Democrats elected three new Bush Dog members from Indiana and two from Ohio.  That gave the region’s Democrats a purplisch cast (9 of 39 Democrats are Bush Dogs,23.1%).  Most of the contested seats this time around represent more urban or at least suburban areas and the results will probably be more reliable votes as well as more Democratic members.  Nine of the region’s 12 Senators are Democrats and Minnesots Republicn Norm Coleman is facing a tough challenge this cycle.

That leaves us with the three Republican leaning regions.  Hopes are highest for the Mountains.  Last cycle Democrats picked up two seats in Arizona and one in Colorado.  This year, hopes center more on New Mexico (two seats) and Rick Renzi’s seat in Arizona.  A three seat piclup would change the delegation from 11-17 in favor of the Republicans to a flat footed tie.  Both Nevada seats and the At Large seats in Wyoming and Montana plus ID-2 have also been mentioned.

Bill Clinton carried three of these states (Arizona, Nevada, and New Mexico in 1996 and five in 1992 when Ross Perot muddied up the waters (AZ, NM, NV, MT, CO).

Democrats have good chances for a Senate seat in New Mexico and one in Colorado.  That would even up the region’s Senate vote to 7-7.

The Plains is a rgion greatly helped by the oddities of US politics.  Iowa’s caucuses make the region important to a whole corps of Presidential wannabes in the US Senate.  Two Senate seats a piece certainly help the Dakotas.

With the notable exceptions of Iowa and Missouri most of the rest of the area produces either conservative Democrats or very conservative Republicans.

The South remains the Republicans key region although their electoral strength has probably peaked out.  Racially-based gerrymanders have created a series of sprawling majority minority districts that have been used to dilute Democratic strength in Congress.  No clearer example exists than the combo of VA-2 and VA-3.  Two more geographically compact districts would produce two pretty strong Democratic districts.  Instead, VA-2 skips many of the black areas in the VA. Beach-Norfolk Hampton roads area and Bobby Scott’s third district edges aroundto include most of Richmond a lot of rural areas and strategically picked, heavily Democratic areas of Hampton Roads.

Last cycle, Republicans lost two seats in Florida, one in North Carolina, one in Kentucky, and two in Texas.  Their current 82-58 edge in the South may well shrink again as Democrats guard several seats in Texas and two in Georgia but eye open seats in Louisiana and rematches in FL-13 and NC-8 as well as actual opportunities in places like Virginia and Kentucky.

Southern Democrats provide the margin that put Democrats back in the Speaker’s chair and the Senate Majority Leader role.  This remains a heavily Republican area for Presidential elections (Republicans won all 13 states for 166 electoral votes).  If Democrats can win three or four of these states they most certainly will win the Presidential election (Virginia, Florida, Arkansas, West Virginia are leading candidates) in part because any candidate who does that is likely to win Ohio as well.

As for the depressing numbers:

House (D 58,R 82, 41.4%)

Senate (D 7, R 19, 26.9%)

Governors (D 6, R 7, 46.2%)

Pr4sidential (13-0 on states, 166-0 on electoral votes)